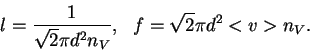Teoría Cinética de los gases

-Todos los materiales de la Naturaleza están compuestos por moléculas y átomos.

-Las componentes microscópicas obedecen las leyes de Newton.

-Sus movimientos son aleatorios.

Gas Ideal

Consideremos N moléculas moviéndose libremente en un recipiente cúbico de lado a, orientado a lo largo de los ejes cartesianos.

Al chocar una molécula con una pared perpendicular al eje x cambia su momentum en:

$$\Delta p_x=-2mv_x$$

El tiempo que demora la molécula en chocar con la misma pared es:

$$\Delta t=\frac{2a}{v_x}$$

Por lo tanto, la fuerza ejercida por la molécula sobre la pared, de acuerdo a la Tercera Ley de Newton, es:

$$F=mv_x^2/a$$

Dado que hay N moléculas y que la presión es $F/A$ , tenemos que:

$$PV=mN\bar v_x^2$$

donde $\bar v_x^2$ es el promedio del cuadrado de la componente x de la velocidad de una molécula en el gas. Dado que las moléculas se mueven aleatoriamente, debe ser que:

$$\bar v_x^2=\frac{1}{3}\bar v^2 (*)$$

donde $\bar v^2$ es la velocidad cuadática media de una molécula en el gas.

Esto es:

$$PV=\frac{1}{3}mN\bar v^2$$

Comparando con la ecuación de estado del gas ideal $PV=Nk_B T$ , obtenemos la importante relación:

$$\bar K=\frac{1}{2}\bar v^2=\frac{3}{2} k_BT$$

Esta relación permite interpretar la temperatura como la energía cinética media de una molécula en el gas. Esta interpretación es general y se aplica a sólidos y líquidos también.

Recordando (*), se tiene que:

$$\frac{1}{2}mv_x^2=\frac{1}{2}mv_y^2=\frac{1}{2}mv_z^2=\frac{1}{2}k_B T$$

Esto se conoce como el Teorema de Equipartición de la Energía: La contribución a la energía interna de un gas de cada grado de libertad de sus moléculas es $\frac{1}{2}k_B T$

Calor Específico Molar de un gas ideal

Se define:

$$Q=nC_V \Delta T (volumen constante) \ Q=nC_P\Delta T (presion constante)$$

Consideremos un proceso a volumen constante. Por lo tanto W=0. La Primera Ley da:

$$\Delta U=Q=nC_V\Delta T$$

Si $C_V$ es constante tenemos que:

$$U=nC_V T$$

Esta relación se aplica a todos los gases ideales, sean monoatómicos o no.

Para cambios infinitesimales de temperatura se tiene:

$$C_V=\frac{1}{n}(\frac{\partial U}{\partial T})_V$$

Para un gas monoatómico se encuentra:

$$C_V=\frac{3}{2}R$$

Esta predicción calza bien con los gases reales monoatómicos.

Consideremos un proceso a presión constante. Se tiene:

$$\Delta U=nC_V\Delta T=Q-P\Delta V=nC_P\Delta T-nR\Delta T$$

Esto es:

$$C_P-C_V=R$$

Esta conclusión se aplica a cualquier gas ideal.

Para un gas ideal monoatómico se tiene:

$$\gamma=\frac{C_P}{C_V}=1.67$$

Procesos adiabáticos para un gas ideal

En un proceso adiabático no hay intercambio de calor. De la primera ley:

$$dU=nC_V dT=-W=-PdV$$

pero:

$$PdV+VdP=nRdT$$

Despejando dt y recordando que $C_P-C_V=R$ , tenemos:

$$\gamma\frac{dV}{V}+\frac{dP}{P}=0$$

Por lo tanto:

$$PV^\gamma=constante$$

La equipartición de la energía

Se puede mostrar que como consecuencia de la Física clásica, es válido el teorema de Equipartición de la energía mencionado anteriormente. Veamos ahora como se aplica a gases ideales:

i) Molécula monoatómica: 3 grados de libertad(traslación). $U=3\times \frac{1}{2} k_B T$ . $C_V=\frac{3}{2}R$ .

ii) Molécula biatómica:3 grados de libertad(traslación)+ 2 grados de libertad (rotación con un eje invariante), $U=5\times \frac{1}{2} k_B T$ . $C_V=\frac{5}{2}R$ .

iii)Molécula poliatómica:3 grados de libertad(traslación)+ 3 grados de libertad (rotación arbitraria), $U=6\times \frac{1}{2} k_B T$ ...

iv) Molécula diatómica con energía vibracional(resorte):3(t)+2(r)+2(v)=7. Esto implicaría $C_V=\frac{7}{2}R$ , lo que no concuerda con los experimentos.

Además $C_V$ depende de la temperatura, lo que implica que los diferentes grados de libertad se van excitando a diferentes energías. Esto se puede entender sólo en el marco de la Mecánica Cuántica.

-Cuantización de la energía: Se requiere un quantum de energía adecuado para excitar los grados de libertad. Si la temperatura es muy baja sólo los grados de libertad traslacionales contribuyen al calor específico.

v)Para sólidos a altas temperaturas: Los átomos vibran en torno a sus posiciones de equilibrio. Cada uno tiene una energía: $E=\frac{1}{2}m (v_x^2+v_y^2+v_z^2)+\frac{1}{2}k(x^2+y^2+z^2)$ . Esto es 6 grados de libertad. Esto da $C_V=3R$ (Ley de Dulong-Petit). Esto falla a bajas temperaturas donde se requiere la Mecánica Cuántica.

Ley de las atmósferas

Determinemos como varía la presión con la altura sobre la superficie de la Tierra. Suponemos que es un gas ideal y que la temperatura es constante.

Sea y la altura sobre la superficie de la Tierra y $n_V$ el número de moléculas por unidad de volumen. Se tiene:

$$dP= -mgn_V dy$$

pero

$$P=n_Vk_BT$$

Lo que implica:

$$n_V(y)=n_0e^\frac{-mgy}{k_BT}$$

Esta última fórmula se llama ley de las atmósferas.

Para la presión se tiene

$$P=P_0e^\frac{-mgy}{k_BT}$$

Se define el valor promedio

$$<A(y)>=\frac{\int_0^\infty A(y) n_V(y)}{\int_0^\infty n_V(y)}$$

Ej:

- $<y>=\frac{k_B T}{mg}$

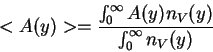
-Energía potencial gravitacional media:$<U>=k_B T$ .

La distribución de Boltzmann

$$n_V(E)=n_0e^\frac{-E}{k_BT}$$

Esto es el número de moléculas por unidad de volumen que tienen energía E. Es válido también en Mecánica Cuántica.

Ejercicio:

Excitación térmica en un átomo con dos niveles.

Distribución de velocidades

En 1860 J.C. Maxwell descubrió la ley de distribución de velocidad de las moléculas de un gas.

Sea $N_v$ tal que el número de moléculas del gas con módulo de la velocidad entre v y v+dv es:

$$dN=N_vdv$$

De la Ley de Boltzmann, el número de moléculas(por unidad de volumen) que tiene energía (cinética), entre E y E+dE es:

$$dN=N_0 e^\frac{-mv^2/2}{k_BT}d^3v$$

Escribiendo la última expresión en coordenadas esféricas para v y recordando que hay N moléculas de gas, lo que fija $N_0$ , se tiene la distribución de Maxwell:

$$N_v=4\pi N (\frac{m}{2\pi k_B T} )^{3/2} v^2e^\frac{-mv^2}{2 k_BT}$$

Ejercicio:

-Encontrar la velocidad más probable. R: $v_{mp}=\sqrt{\frac{2k_B T}{m}}$

-La rapidez promedio. R: $<v>=\sqrt{\frac{8k_B T}{\pi m}}$

-La velocidad cuadrática media $v_{cm}=\sqrt{<v^2>}=\sqrt{\frac{3k_B T}{m}}$

Trayectoria libre media

Las velocidades promedio de las moléculas que calculamos más arriba son grandes. Entonces por qué los olores en una pieza demoran un tiempo relativamente largo en detectarse? La razón es que las moléculas chocan entre sí. No se propagan en línea recta.

La distancia promedio recorrida por la molécula entre dos choques sucesivos se llama recorrido libre medio l. Para calcularlo imaginemos que las moléculas tienen diámetro d. Se puede ver que dos moléculas chocarán solamente si la distancia entre sus centros es menor a 2d. En forma equivalente podemos pensar que el choque ocurre entre una molécula de radio 2d y otra puntual.

Consideremos el movimiento de la molécula más grande. Su rapidez promedio es $<v>$ . En un tiempo t recorre una distancia $<v>t$ . Durante este tiempo chocará con un n'umero de moléculas:

$$N=n_V <v> td^2\pi$$

Por lo tanto la distancia entre choques sucesivos es:

$$l=\frac{<v> t}{N}= \frac{1}{\pi d^2 n_V}$$

-frecuencia de choque f= choques por unidad de tiempo=$\pi d^2<v>n_V$ .

-tiempo libre medio=$1/f$ .

Hemos supuesto que las moléculas que chocan con la grande son estacionarias. Si incluimos su movimiento se tiene:

$$l=\frac{1}{\sqrt{2} \pi d^2 n_V}, f=\sqrt{2}\pi d^2<v>n_V.$$