Pontificia Universidad Católica de Chile Facultad de Física ONDAS Y CALOR Segundo  Semestre 2002 GUIA 1: Oscilaciones

1.- Un bloque de masa M se encuentra sobre un carro al cual se le comunica un movimiento armónico simple de frecuencia 0.5 Hz, como muestra la figura.  Si el coeficiente de roce estático entre el bloque y la superficie del carro es 0.5,  ¿Cuál es la máxima amplitud de oscilación posible, tal que el bloque se mueve conjuntamente con el carro, sin deslizar sobre éste?  Resp.:  0.5 m.

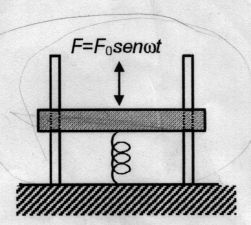
2.- Una plataforma de 10 kg está sostenida por un resorte de constante k = 40 N/m y se encuentra sometida a una fuerza periódica de magnitud máxima 5 N.  Al oscilar, la masa desliza a lo largo de dos barras, de modo que el coeficiente de amortiguamiento es 5 N·s/m.  Encuentre:  a) La frecuencia natural de oscilación de la plataforma para el caso en que no hay amortiguamiento.  b) la frecuencia de la fuerza periódica que hace máxima la amplitud de oscilación.  c) la máxima amplitud de oscilación de la plataforma.  d) el Q del sistema.  e) el ancho de la curva de resonancia del sistema.  Resp.:  a) 2 rad/s,   b) 1.969 rad/s,   c) 25.75 cm,   d) 4,   e) 0.5 rad/s.

3.- Al soltar libremente una esfera de 3 kg, ésta cae en el aire con una velocidad terminal de 25 m/s (suponga que la fuerza de rozamiento es -bv).  Luego la esfera es unida a un resorte de constante de fuerza k= 400 N/m, y oscila con una amplitud inicial de 20 cm.  a) ¿Cuánto tiempo demora la amplitud en disminuir a 10 cm?  b) ¿Cuánta energía se habrá perdido cuando la amplitud sea 10 cm?  Resp.:  a) 3.5 s,   b) 6 J.

4.- Un oscilador amortiguado tiene una frecuencia w' que es un 10% menor que su frecuencia sin amortiguamiento.  a) ¿En qué factor disminuye su amplitud en cada oscilación?  b) ¿En qué factor se reduce su energía durante cada oscilación?  Resp.:  a) 0.065,   b) 0.004.

5.- Un objeto de 2 kg oscila sobre un resorte de constante elástica k = 400 N/m. La constante de amortiguamiento es b =2 N·s/m.  Este oscilador es accionado por una fuerza sinusoidal de amplitud 10 N y frecuencia angular w = 10 rad/s.  a) ¿Cuál es la amplitud de las oscilaciones?  b) Si se varía la frecuencia de la fuerza impulsora, ¿a qué frecuencia se producirá la resonancia?  c) Encuentre la amplitud de las oscilaciones en resonancia.  d) ¿Cuál es el ancho de la curva de resonancia?  Resp.:  a) 5 cm,   b) 200 rad/s,   c) 50 cm,   d) 1 rad/s.

6.- Una araña de 0.36 gramos de masa está en medio de su tela, que se hunde 3 mm bajo su peso. Estime la frecuencia de la vibración vertical de este sistema.  Resp.:  9.1 Hz.

7.- Encuentre el período de pequeñas oscilaciones de un cilindro de radio r que se rueda sin resbalar en el interior de una superficie curva de radio. Resp.:

8.- Un cilindro delgado de radio R y masa M está suspendido por una cuerda que da vuelta alrededor de él, como indica la figura.  Un extremo de la cuerda está unido a un soporte rígido y el otro a un resorte de constante k.  Determine la frecuencia de oscilación del cilindro, suponiendo que la cuerda no resbala sobre éste. Resp.:

9.- Un cilindro sólido de radio r y masa m cuelga de un resorte de constante k, parcialmente sumergido en agua, como muestra la figura.  Calcule el período para pequeñas oscilaciones del cilindro a lo largo de la vertical. Resp.: , con r la densidad del agua

10.- Encuentre el período de pequeñas oscilaciones de un péndulo simple de largo l y masa m, que se encuentra en el interior de un ascensor, que se mueve a lo largo de la vertical con aceleración ± a.  Discuta el caso en que a = g, en dirección hacia abajo. Resp.:

11.- Una partícula de masa m se mueve en la región x > 0 bajo la acción de la fuerza F = -kx + c/x, donde k y c son constantes positivas.  a) Encuentre la energía potencial de la masa.  b) Determine sus posiciones de equilibrio.  c) Encuentre la frecuencia angular para pequeñas oscilaciones en torno a los puntos de equilibrio. Resp.:

12. La energía potencial de una partícula de masa m está dada por la expresión , donde a y c son constantes positivas.  a) Encuentre la posición de equilibrio estable para la masa m.  b) Encuentre el período de pequeñas oscilaciones en torno al punto de equilibrio. Resp.: