c14

FIS1532 Clase 14
Fecha:23/04/2001

Condensadores en dielectricos

Condensador de placas paralelas conductoras gruesas: D=\sigma \hat z(z crece hacia la carga negativa);E=\sigma/\epsilon\hat z;\phi(d)-\phi(0)=-d \sigma/\epsilon;-V=-d \sigma/\epsilon;C=\epsilon A/d.
Condensador esferico: radio interior a,radio exterior b:E=q/(4\pi\epsilon r^2) ;V=q/(4\pi\epsilon)(a^{-1}-b^{-1}):C=4\pi\epsilon/(a^{-1}-b^{-1})
Condensador cilindrico
Condensadores en paralelo: C=C_1+C_2
Condensadores en serie: C^{-1}=C_1^{-1}+C_2^{-1}

Fuerzas y Torques

Sistema aislado: dW=F.dx; como es aislado dW=-dU(U es la energia electrostatica). Se tiene: F=-\nabla U.Si el sistema puede rotar, se tiene dW=\tau. d\theta. Luego \tau=-U,\theta.
Conductores mantenidos a potencial constante por una fem exterior:dW=dW_b-dU;dU=1/2\sum _j \phi_j dQ_j; dW_b=\sum_j\phi_j dQ_j. Luego dW_b=2dU. Se tiene que F=\nabla U (Notar la diferencia de signo entre las dos situaciones). Similarmente \tau=U,\theta.

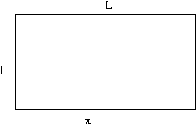
Ejercicio 1:Considere un condensador de placas paralelas aislado. En este se introduce un dielectrico de constante K. Encuentre la fuerza que actua sobre este.

Asignamos densidades de carga $\sigma_1$ y $\sigma_2$ a las dos regiones. Como la diferencia de potencial es la misma (un conductor forma una superficie equipotencial), se encuentra . Esto es $\frac{\sigma_1}{\epsilon_1}=\frac{\sigma_2}{\epsilon_2}$ . La energia contenida en el volumen es:

$\begin{displaymath}U=\frac{1}{2} \frac{Q^2d}{l\epsilon_0(K_1x+(L-x)K_2]}\end{displaymath}$

$\begin{displaymath}F=\frac{1}{2} \frac{Q^2d(K_1-K_2)}{l\epsilon_0(K_1x+(L-x)K_2]^2}\end{displaymath}$

Esta fuerza tira al dieléctrico hacia el interior del condensador.

Ejercicio 2: Considere un condensador de placas paralelas cuyas placas estan conectadas a los polos de una bateria. En este se introduce un dielectrico de constante K. Encuentre la fuerza que actua sobre este.

Si el proceso sucede a diferencia de potencial constante V se tiene:

$\begin{displaymath}U=\frac{lV^2\epsilon_0((L-x)K_2+xK_1)}{2d}\end{displaymath}$

luego

$\begin{displaymath}F=\frac{lV^2\epsilon_0(K_1-K_2)}{2d}\end{displaymath}$

Nuevamente la fuerza es hacia el interior del condensador.

Ejercicio 3: Un capacitor de placas paralelas se llena con dos dieléctricos en serie horizontal con constantes dieléctricas k1 y k2 de largos L1 y L2 y de ancho l . Las placas están separadas una distancia d. Encontrar C.

R:C=\epsilon_0 l(k1L1+k2L2)/d.

Ejercicio 4: Un capacitor de placas paralelas se llena con dos dieléctricos en serie vertical con constantes dieléctricas k1 y k2 de espesor d1 y d2(d1+d2=d). Encontrar C.

R: C=\epsilon_0 A/(d1/k1+d2/k2)