c5

FIS1532 Clase 5
Fecha:21/03/2001

Divergencia en coordenadas cartesianas: $\begin{displaymath}\vec\nabla \vec A(\vec x)=div \vec A(\vec x)=\frac{\partial ......rac{\partial A_y}{\partial y}+\frac{\partial A_z}{\partial z}\end{displaymath}$

Teorema de Gauus(Teorema de la divergencia)

Consideremos un paralelepípedo recto de lados a,b,c.. La integral de volumen de divA en el cubo se puede descomponer en tres integrales. Evaluamos explícitamente la correspondiente a la integral en x:

$\begin{displaymath}\int_0^b dy\int_0^c dz \int_0^a dx\frac{\partial A_x}{\parti......_0^b dy\int_0^c dz (A_x(a,y,z)-A_x(0,y,z))=\Phi(x=a)+\Phi(x=0)\end{displaymath}$

Las otras se evalúan en forma similar.

Para demostrar el teorema en general, cubrimos el volumen V con paralelepípedos rectos pegados a lo largo de una cara. Es fácil ver que el flujo a través de las caras comunes se cancela de a pares, quedando sólo el flujo a través de las caras externas de la suma de los dos cubos. Finalmente, pasando al límite continuo se ve que sólo permanece el flujo a través de la superficie S.

Conductor aislado

E=0 al interior del conductor, debido a F=0, en equlibrio electrostático.
E tangencial a la superficie del conductor=0, por la misma razón.
Sólo existe la componente de E normal a la superficie en cada punto.
Usando la ley de Gauss se muestra que no hay cargas al interior del conductor. Indic: Usar una superficie cerrada S infinitesimalmente cercana a la superficie del conductor, pero sumergido en éste. E=0 en S.
Todas las cargas están sobre la superficie del conductor.

Aplicaciones de la Ley de Gauss (continuación)

Distribución de carga con simetría esférica. Encontrar E
Franja conductora infinita, cuya superficie exterior (dos planos paralelos) está uniformemente cargada con densidad superficial \sigma
- Usar la ley de Gauss directamente
- Resolver primero el caso de un plano infinito uniformemente cargado: E=\sigma/(2\epsilon_0)sgn(z)
- Usar el principio de superposición para encontrar la solución al problema original.
- AQUI ABAJO SE ILUSTRA EL EXPERIMENTO QUE MUESTRA QUE LA CARGA SE ACUMULA EN LA SUPERFICIE EXTERIOR DE UN CONDUCTOR.

POTENCIAL ELECTROSTATICO

Definición de rotor en coordenadas cartesianas

$\begin{displaymath}(rot \vec A(\vec x))_i=(\vec\nabla \times \vec A(\vec x))_i=\epsilon_{ijk}\frac{\partial A_j}{\partial x^k}\end{displaymath}$

donde el símbolo de Levi-Civita es:

$\begin{displaymath}\epsilon_{ijk}=signo de la permutacion (ijk)\end{displaymath}$
Definición de gradiente en coordenadas cartesianas

$\begin{displaymath}grad \phi=\vec\nabla\phi=\frac{\partial \phi}{\partial x} \h......i}{\partial y} \hat y+\frac{\partial \phi}{\partial z} \hat z\end{displaymath}$
Teorema del rotor (Stokes). Enunciado, sin demostración.

$\begin{displaymath}\int_C \vec A(\vec x).d\vec x=\int\int_S \nabla\times\vec A(\vec x).\hat n dS\end{displaymath}$
Ejercicio: rot(grad)=0
Proposición: Si en una región rot A=0, implica que A=grad\phi. Definir \phi=\int_C A.dx y mostrar que \phi no depende de C. Es un campo escalar (sólo depende de \vec x).
Usar la ley de Coulomb para mostrar que E=-grad \phi con \phi(x)=\int dx'' \rho(x'')/(4\pi\epsilon_0|x"|)
Este \phi es el potencial electrostático.
Teorema del trabajo y la energía: Consideremos el movimiento de una carga puntual de masa m y carga q en presencia de un potencial electrostático \phi. Se tienen dos manera de calcular el trabajo realizado por el campo eléctrico para mover la carga de A a B a lo largo de una curva C (El trabajo no depende de la curva, en este caso de fuerzas conservativas)
- W_{AB}=-q\phi_B+q\phi_A
- W_{AB}=mv_B^2/2-mv_A^2/2
- Se tiene que mv^2/2+q\phi se conserva. Por lo tanto q\phi es la energía potencial electrostática.
  
  Por lo tanto se tiene que la energía potencial electrostática se define por:

El potencial electrostático se obtiene de la energía potencial:

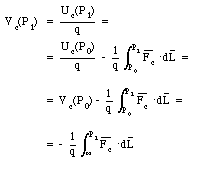
Para una carga puntual q' se encuentra:

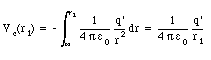
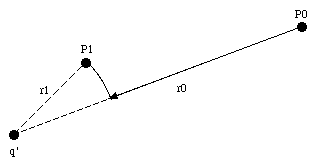
Notar que, en este caso el potencial se anula en infinito.

La energía potencial es:

Ejercicio: Encontrar el potencial electrostático de una línea infinita uniformemente cargada con una densidad lambda.

Resp: El campo eléctrico se encuentra aplicando la ley de Gauss a un cilindro de largo L, con manto paralelo a la línea, y centrado en ésta. El manto se encuentra a una distancia r de la línea. Se obtiene: E=lambda/(2\pi\epsilon_0 r). De la definición del potencial electrostático, elegiendo una curva radial da: \phi(r)=-lambda ln(r/r_0)/(2\pi\epsilon_0). Notar que aquí el potencial se anula en r_0 y no en infinito. Esto se debe a que hay cargas en infinito.