Refrigeradores

Un refrigerador es una máquina de calor que funciona a la inversa. Esto es : Absorbe calor de un depósito a temperatura $T_c$ y libera calor a un depósito a mayor temperatura $T_h$. Para lograr esto debe hacerse un trabajo W sobre el sistema. La experiencia muestra que esto es imposible hacerlo con W=0.

Se define la eficiencia de un refrigerador como:

$$\eta=\frac{Q_c}{W}$$

donde $Q_c$ es el calor extraído del depósito frío y W es el trabajo hecho por el refrigerador.

Segunda Ley de la Termodinámica (enunciado de Clausius): Es imposible construir una máquina cíclica cuyo único efecto sea la transferencia continua de energía de un objeto a otro de mayor temperatura sin la entrada de energía por trabajo.

Se puede mostrar que estos enunciados de la Segunda Ley son equivalentes.

La máquina de Carnot

Una máquina térmica cualquiera no puede superar la eficiencia de una máquina de Carnot funcionando entre dos depósitos de energía idénticos.

Para ver esto, considere dos máquinas térmicas que operan usando los mismos depósitos de energía. Una es una máquina de Carnot, con eficiencia $e_C$, y la otra tiene eficiencia $e>e_C$. La máquina más eficiente se usa para hacer funcionar la máquina de Carnot como un refrigerador de Carnot. Para hacer esto se equipara la salida en trabajo de la máquina más eficiente con la entrada en trabajo del regrigerador. El efecto neto es transferir calor del depósito frío al caliente sin realizar trabajo. Esto viola la Segunda Ley (Clausius). Lo que distingue el ciclo de Carnot (que veremos inmediatamente) es que es reversible. Por lo tanto, el mismo argumento expuesto más arriba muestra que todos los ciclos reversibles igualan la eficiencia del ciclo de Carnot (nunca la superan).

El ciclo de Carnot

Considere un gas ideal.

1. Proceso $A->B$ es una expansión isotérmica a $T=T_h$. Se absorbe energía $Q_h$ y se realiza un trabajo $W_{AB}$.

2. Proceso $B->C$ es una expansión adiabática. La temperatura del gas disminuye a $T_c$ y realiza un trabajo $W_{BC}$.

3. Proceso $C->D$ es una compresión isotérmica a $T=T_c$. Se libera energía $Q_c$ hacia el depósito, y el trabajo realizado sobre el gas es $W_{CD}$.

4. Proceso $D-> A$ es una compresión adiabática. La temperatura del gas aumenta a $T_h$ y el trabajo efectuado sobre el gas es $W_{DA}$.

El trabajo neto realizado por el gas en este proceso cíclico es el área encerrada en la figura.

Mostraremos que la eficiencia de una máquina de Carnot es:

$$e_C=1-\frac{T_c}{T_h}$$

En $A->B$ se tiene:

$$Q_h=W_{AB}=nRT_hln\frac{V_B}{V_A}$$

En $C->D$ se tiene:

$$Q_c=\vert W_{CD}\vert=nRT_cln\frac{V_C}{V_D}$$

Notar que los Q de una máquina térmica se consideran positivos.

Por lo tanto:

$$\frac{Q_c}{Q_h}=\frac{T_c}{T_h}\frac{ln(V_C/V_D)}{ln(V_B/V_A)}$$

Para un proceso adiabático se tiene que:

$$TV^{\gamma-1}=constante$$

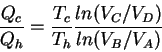
Por lo tanto:

$$T_hV_B^{\gamma-1}=T_cV_C^{\gamma-1}\,\ T_hV_A^{\gamma-1}=T_cV_D^{\gamma-1}$$

lo que implica:

$$\frac{V_B}{V_A}=\frac{V_C}{V_D}$$

luego:

$$\frac{Q_c}{Q_h}=\frac{T_c}{T_h}$$

Motores de Gasolina y Diesel

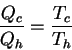
Un motor de gasolina se aproxima usando el ciclo de Otto:

1. Durante la carrera de admisión $O->A$ el pistón se mueve hacia abajo, y una mezcla gaseosa de aire y combustible se introduce en el cilindro a presión atmosférica. El volumen aumenta de $V_2$ a $V_1$.

2. Durante la carrera de compresión $A->B$ el pistón se mueve hacia arriba, la mezcla de aire-combustible se comprime adiabáticamente del volumen $V_1$ al $V_2$ y la temperatura aumenta de $T_A$ a $T_B$. El trabajo realizado por el gas es negativo.

3. En $B->C$ la combustión ocurre cuando se enciende la chispa de la bujía. Esta no es una de las carreras del ciclo porque ocurren en un período muy breve. La temperatura y presión del gas aumentan considerablemente, pero el volumen permanece prácticamente constante, por lo que el gas no realiza trabajo.

4. En la carrera de potencia(expansión) $C->D$, el gas se expande adiabáticamente de $V_2$ a $V_1$, con un descenso de temperatura de $T_C$ a $T_D$.

5. En el proceso $D-> A$ una válvula de escape se abre conforme el pistón alcanza el final de su viaje y la presión disminuye repentinamente.

6. En la carrera de escape $A->O$ el pistón se mueve hacia arriba mientras la válvula de escape permanece abierta. Los gases reciduales se expulsan a presión atmosférica y el volumen disminuye de $V_1$ a $V_2$.

Si se representa la mezcla aire-combutible por un gas ideal, se tiene la eficiencia del ciclo de Otto:

$$e=1-\frac{1}{(V_1/V_2)^{\gamma-1}}$$

$V_1/V_2$ es la relación de compresión

Eficiencia del ciclo de Otto

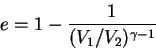
Trabajo neto(Primera Ley):

$$W=Q_h-Q_c$$

Pero:

$$Q_h=nC_V(T_C-T_B), \ \ Q_C=nC_V(T_D-T_A)$$

Esto es:

$$e=1-\frac{T_D-T_A}{T_C-T_B}$$

Para procesos adiabáticos se tiene que

$$TV^{\gamma-1}=constante$$

Luego

$$T_AV_A^{\gamma-1}= T_BV_B^{\gamma-1} , \ T_CV_C^{\gamma-1}= T_DV_D^{\gamma-1}$$

Recordando que, $V_A=V_D=V_1$ y $V_D=V_C=V_2$, se tiene que:

$$\frac{T_D-T_A}{T_C-T_B}=\left(\frac{V_2}{V_1}\right)^{\gamma-1}$$

Bombas de Calor y Refrigeradores

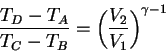
Coeficiente de realización(CDR):

$$CDR(modo de calentamiento)=\frac{Q_h}{W}$$

$$CDR(modo de enfriamiento)=\frac{Q_c}{W}$$

Entropía

Ahora definimos una nueva función de estado:

$$dS=\frac{dQ_r}{T}$$

Para utilizar esta definición debe elegirse un proceso reversible que conecte el estado inicial con el final.

Para un ciclo reversible se tiene que:

$$dS=0$$

Para un proceso real (no reversible) se tiene:

$$dS>0$$

Este es un nuevo enunciado de la Segunda Ley de la Termodinámica, equivalente a los dados con anterioridad.

Para un ciclo de Carnot se tiene:

$$\Delta S=\frac{Q_h}{T_h}-\frac{Q_c}{T_c}$$

Pero

$$\frac{Q_h}{T_h}=\frac{Q_c}{T_c}$$

con lo que

$$\Delta S=0$$

Dado que la entropía es una función de estado, se tiene, para todo ciclo reversible:

$$dS=0$$

Proceso Reversible y Cuasiestático para un gas ideal

i($T_i,V_i$)->f($T_f,V_f$):

$$dQ_r=nC_VdT+nRT\frac{dV}{V}$$

y

$$\frac{dQ_r}{T}=nC_V\frac{dT}{T}+nR\frac{dV}{V}$$

Por lo tanto:

$$\Delta S=nC_Vln\frac{T_f}{T_i}+nRln\frac{V_f}{V_i}$$

Esto muestra que S es una función de estado.

Cambios de Entropía en Procesos Irreversibles

Se debe elegir un proceso reversible que conecte los estados inicial y final.

Segunda Ley: La entropía total de un sistema aislado que se somete a un cambio nunca puede disminuir

Proceso reversible: $dS=0$

Proceso irreversible: $dS>0$.

Muerte Térmica del Universo: Temperatura y densidad uniformes.

Cambio de Entropía en una Expansión libre

$$\Delta S=nRln\frac{V_f}{V_i}$$